Psychic Modeling: The Problem of Identifying Minimal Lottery Ticket Set

For a long time I was planning to find some time to work through the book “The Algorithm Design Manual” by Steven Skiena[1]. It is well recognized by many as a great source of algorithm wisdoms.

When that day has come, soon I discovered that I can’t get past Chapter 1. One thing threw me out of balance, right from the beginning. That was the problem that the author of the book, Mr. Skiena, offers to solve to his reader, under the implementation exersize section of the first chapter.

I’ll try to make a claim that neither the book nor the referenced paper present an optimal working solution for the given exercize. And for that reason it is likely to be a source of confusions to many readers.

Problem statement

Below is my brief paraphrase of the problem description

Imagine a lottery system with the following rules:

Imagine, there are some people (in the book they are called psychics, I will call them lottery insiders) who can guarantee you the following edge:

The question is: Given the input numbers: `N <= R <= J <= L`, What is the minimum set of tickets you need to buy, in order to guarantee to have at least one winning ticket?

For a complete problem description, I recommend refering to a chapter from the book[2].

Reasoning

First of all, the book does not even attempts to present the correct solution to a mentioned problem. It only provides an incorrect solution, in an attempt to emphasize the importance of the problem modeling before coming up with the final algorithm design.

Lotto Pseudocode
Fig. 1: Lotto Pseudocode

The book claims that the general outline of that incorrect solution still holds for the real problem and with some minor modification, it must be obvious enough how to make it solve the original problem.

All we must fix is which subsets we get credit for covering with a given set of tickets. After this modification, we obtained the kind of results they were hoping for.

I read this sentence a hundred times, thinking that the trick to the solution carefully covered within these words:

All we must fix is which subsets we get credit for covering with a given set of tickets.

As I found out, it was naive to assume so. I think this sentence is misleading. Which subsets are we talking about here? `NR`-subsets? `NL`-subsets?

Turns out, the right answer to this question is `NJ`-subsets, (or `JP`-subsets of `NP`-subsets to be more precise), even though I'm not sure if that what was intended. I will show later why I believe it is the case. The problem is that the algorithm described in the book completely disregards `J` and its importance for the working solution. In a similar manner as the paper disregards the importance of `R`, hence leading to the incorrect algorithm.

Paper

In the chapter notes, the book says: our solution to the lotto ticket set covering problem is presented in more detail here[3].

The referenced paper introduced the notion of two subsets overlapping each other which is crucial to come to a working solution.

What puzzled me, is why is the algorithm presented in the paper disregard R completely, as if nothing depends on it? Even when they presented a complexity estimate, the `R` is missing from the equation.

It almost tricked me to believe that is the case. In fact, in the pseudocode algorithm from the book, it is `J` that is missing. I was starting to believe, that these are just two equivalent algorithms, in which you can either disregard `R` or `J` completely and still being able to solve the problem optimally.

However, that turned out to be not the case.

Framework

I will try to present here my framework for thinking about the problem, together with a few examples to make it easier to follow.

First, let's see what each of the subsets means:

$N \choose R$ - these are all possible combinations of tickets with numbers, given that we follow the insiders lead.

We know that `J` out of `N` numbers will be in a master/winning ticket, so:

$N \choose J$ - gives us every possible combination of predicted numbers that can occur in a winning ticket. We need to cover them all with our bought tickets if we want to be certain to win.

Now I want to emphasize what we wean by covering a `NJ` with a `NR`. We can consider it covered if our ticket from subset NR cover at least one item from `JL`-subset of `NJ`-item.

$N \choose L$ - every possible combination that may appear in a master/winning ticket. Note that this subset doesn’t reflect anything important by itself. You don’t need to cover them all to be able to win.

$J \choose L$ - every combination of `L` numbers from `J`, any of it will lead you to win. When covering `NJ`-subsets, it is enough to cover just a single `JL`-subset of `NJ`-item, to consider it covered. Any `L` numbers from `JS` will make the ticket holder a winner.

Instead of covering items of `NJ`-subsets in terms of covering `JL`-subsets of `NJ`-items, we could use a more convenient technique: if the intersection of `NJ`-item with a given ticket is`>= J`, that means we cover at least one item from its `NL`-subset.

The goal is to cover all `NJ`-subsets with your set of tickets.

Lower bound

To calculate the lower bound for the number of tickets, we can have the following question:

How many other `NJ`-subsets have a coverage of at least `L` with any given `NJ`-subset?

The covered `NJ`-subsets must have at least `L` numbers in common with the first one, the rest is taken from the `N-J` other numbers.

So, in the best case, you’ll be able to cover this number of `NJ`-subsets:

$$ {\sum \limits_{L <= i <= J}} {R \choose i} {N - R \choose J - i} $$

You will not be able to cover that much with every ticket, but it’s useful to have the lower bound in mind.

Examples

This pair of inputs shows the important distinction that clarifies the reasoning:

Lotto Pseudocode
Fig. 2: Example 5-4-3-2

Lotto Pseudocode
Fig. 3: Example 5-3-3-2

Implementation approach

As we can see, general outlines from the book still hold true:

The problem statement is a variance of the NP-complete set cover problem, which means there is no efficient algorithm for solving it (by solving we assume identifying the smallest possible ticket set). We could still have close enough answer with the use of randomization in our algorithm.

Results

To indicate the difference between results from the proposed algorithm and the one described in a paper, I run it on the same sets of input values as presented in the paper, and put them for comparison.

My results:

N R J L Lower Bound No of Tickets Time / sec
15 5 5 4 59 133 28
15 5 5 5 3003 3003 85
15 6 5 4 22 61 12
15 6 5 5 501 784 58
15 6 6 6 5005 5005 254
18 5 5 4 130 330 156
18 6 5 4 47 144 29
18 10 7 6 18 74 68

Paper results:

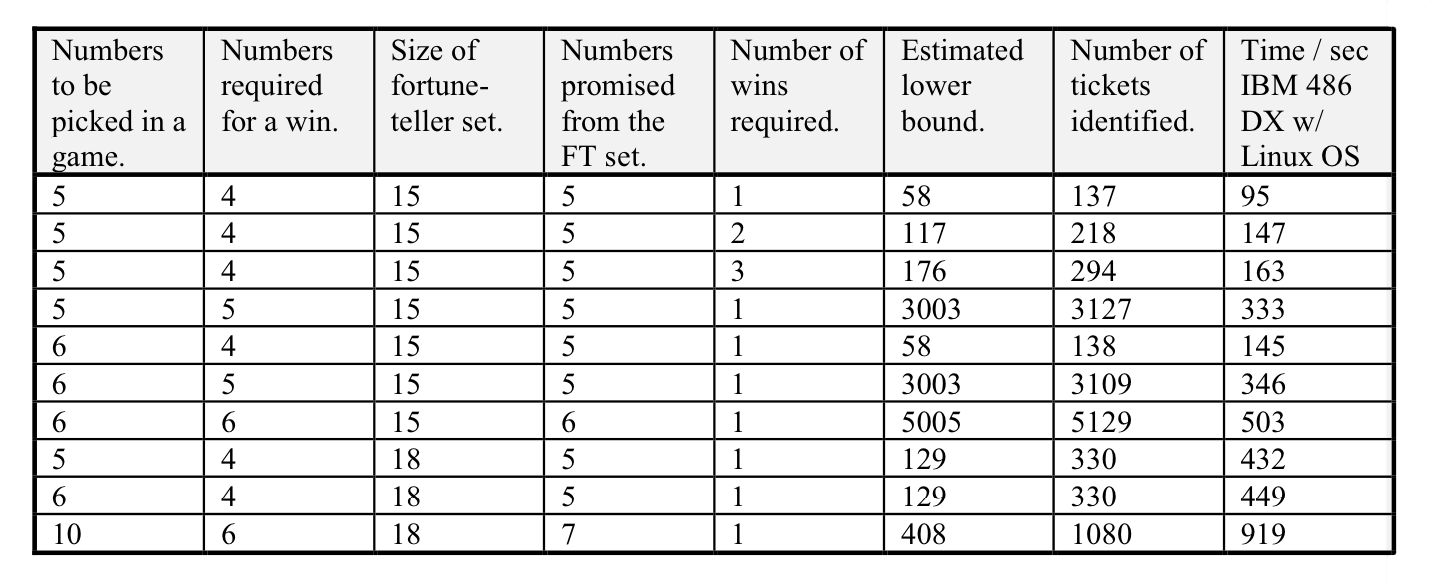
Lotto Table1
Fig. 2: Lotto Paper Results Table

It can be seen clearly, the improved algorithm yields considerably smaller ticket sets when `R > J`.

In cases when `R = J`, the improvements are either small or neglectable.

In certain cases, when we have to include every ticket into our set, sanity checks in place prevents us from buying extra tickets when they do not cover any `NJ`-subsets for us, as in the case when: `N = 15` and `R = J = L = 5`.

Code

My C++ drafts with a solution could be found here[6]. It might require some tuning for the best performance, though I believe it is good enough to meet the requirements of a given problem.

There is a test function validating the wining ticket set, by running a number of random experiments at drawing a master ticket and outlining a ticket from the set that won the jackpot.

vector_2d_t lotto_ticket_set(int n, int k, int j, int l, int SAMPLE_LEN) {
    vector_2d_t ticket_set;

    vector_2d_t nj_subsets = combine(n, j);
    vector<bool> v(nj_subsets.size(), false);

    cout << "NJ subsets size: " << v.size() << "\n";

    int covered_so_far = 0;
    int max_coverage = 0;
    vector<bool> temp_v = v;

    cout << "Picking tickets...\n" << "---\n";

    while (covered_so_far != v.size()) {
        max_coverage = 0;
        vector<int> max_coverage_ticket;

        for (int i = 0; i < SAMPLE_LEN; i++) {
            vector<int> k_sample = sample_k_subset(n, k);
            temp_v = v;

            int covered = count_coverage(nj_subsets, k_sample, temp_v, j, l);

            if (covered > max_coverage) {
                max_coverage = covered;
                max_coverage_ticket = k_sample;
            }
        }

        if (max_coverage != 0) {
            covered_so_far += max_coverage;
            count_coverage(nj_subsets, max_coverage_ticket, v, j, l);

            ticket_set.push_back(max_coverage_ticket);
        }

        cout << "Covered: " << covered_so_far << " out of " << v.size()
             << " (" << ticket_set.size() << ")\n";
    }

    return ticket_set;
}

Conclusion

It is worth noting, that in the exercises section of the book, this problem 1-27 has given the complexity of 5 out of 10. This can only mean one thing: things are about to get more surprising.

Footnotes

  1. ^ The Algorithm Design Manual by Steven S Skiena, 2nd ed. 2008, on Amazon
  2. ^ Chapter in book: War Story: Psychic Modeling
  3. ^ DOCX: F. Younas and S. Skiena. Randomized algorithms for identifying minimal lottery ticket sets,  Journal of Undergraduate Research, 2-2 (1996) 88-97. Note that it’s in .docx, I converted it to .pdf[4], which you may find more convenient.
  4. ^ PDF: F. Younas and S. Skiena. Randomized algorithms for identifying minimal lottery ticket sets, 1996
  5. ^ Combinatorial Algorithms: Generation, Enumeration, and Search (Discrete Mathematics and Its Applications), by Donald L. Kreher, Douglas R. Stinson, Ch.2.3, p.43
  6. ^ Github Gist: psychic-mode.cpp